Urabe Lab. |1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25|Epilogue　

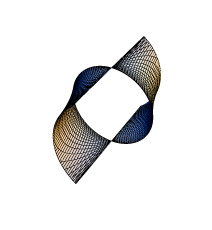
g1 = ParametricPlot3D[ {Cos[u]Cos[v], Tan[v]Cos[u]Sin[v], Sin[u]}, {u, -Pi/2, Pi/2}, {v, -Pi/2 + 0.01, Pi/2 - 0.01}, PlotRange -> {{-Pi/2, Pi/2}, {-Pi/2, Pi/2}, {-Pi/2, Pi/2}}, PlotPoints -> {50, 50}, DisplayFunction -> Identity]; g2 = ParametricPlot3D[ {Cos[u]Cos[v], Tan[v]Cos[u]Sin[v], Sin[u]}, {u, -Pi/2, Pi/2}, {v, Pi/2 + 0.01, 3 Pi/2 - 0.01}, PlotRange -> {{-Pi/2, Pi/2}, {-Pi/2, Pi/2}, {-Pi/2, Pi/2}}, PlotPoints -> {50, 50}, DisplayFunction -> Identity]; Show[{g1, g2}, Boxed -> False, Axes -> None, DisplayFunction -> $DisplayFunction]	ParametricPlot3D[ {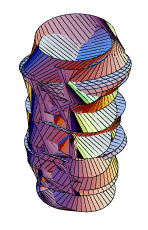Cos[2u]Cos[v]/3, Sin[u]v/u + v/2, Sin[u]Cos[2v]}, {u, -Pi, Pi}, {v, -Pi, Pi}, PlotPoints -> {50, 50}, Boxed -> False, Axes -> None]	ParametricPlot3D[ {Cos[x + y^2] + Cos[x]Sin[y^2], Sin[x] + Cos[x], 2Cos[y] + Sin[y^2]}, {x, 0, 2Pi}, {y, 0, 2Pi}, PlotPoints -> {50, 50}, Boxed -> False, Axes -> None]	ParametricPlot3D[ {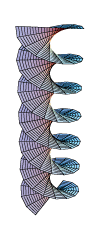u Sin[t], u Cos[t], t/3}, {t, 0, 20}, {u, -1, 1}, PlotPoints -> {50, 25}, Boxed -> False, Axes -> None]

Send your opinions and comments to .