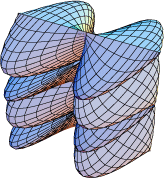
{Cos[u]*Cos[v],
Sin[2u]*Sin[2v], u/4},
{u, -Pi, Pi}, {v, -Pi, Pi},
PlotPoints -> {50, 50},
Boxed -> False,
Axes -> None]
{2 Sin[Cos[2 t^2 + 1]]/(1 + u^2 + Sin[u]),
-Log[t + Sin[t]],
Cos[2 u/3]},
{t, π, 2 π}, {u, π, 2 π},
PlotPoints -> {50, 50},
Boxed -> False,
Axes -> None]
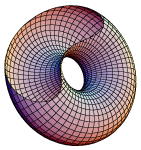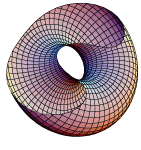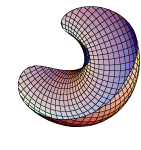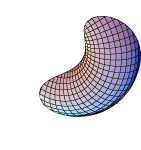
b = 3;
c = Sqrt[a^2 - b^2];
fx[s_, t_] := (a + b*Cos[t])Cos[s];
fy[s_, t_] := (a + b*Cos[t])Sin[s];
fz[s_, t_] := b Sin[t];
fxx[s_, t_] := (c*fx[s, t] + b*fz[s, t])/a;
fyy[s_, t_] := fy[s, t];
fzz[s_, t_] := (-b*fx[s, t] + c*fz[s, t])/a;
Do[ParametricPlot3D[
{fxx[s, t], fyy[s, t], fzz[s, t]},
{t, 0, 2Pi}, {s, -Pi, Pi},
PlotRange -> {
{-(a + b + 1), a + b + 1},
{-(a + b + 1), a + b + 1},
{-(a + b + 1) + i, i}
},
Boxed -> False,
Axes -> None,
PlotPoints -> {31, 61},
ViewPoint -> {0.934, -1.725, 2.757}],
{i, b, -b, -1}]
{2Cos[u](1 + Cos[u]) + 5(1 - Cos[u]/2)(Cos[v + Pi]),
3Sin[u],8(1 - Cos[u]/2)Sin[v]},
{u, 0, 2Pi},
{v, 0, 3Pi},
PlotPoints -> {60, 50},
Boxed -> False,
Axes -> None]
卜部東介研究室に戻る
まで！